DENSIDAD DE CORRIENTE ELÉCTRICA Volumetrica y Supercial Ejemplos y ejercicios resueltos

 

Una vez conocida y estudiada la corriente electrica, vemos que el flujo de carga puede estar contenido en distribuciones volumetricas o superficiales, surgiendo asi las densidades de corriente.

Densidad de corriente ELÉCTRICA volumétrica

Definición

Corriente por unidad de área perpendicular al flujo de carga.

\vec{J}=\rho \vec{v}

I=\dfrac{dq}{dt}_S=\int _S\vec{J}\cdot d\vec{s}

Símbolo

Esta densidad se representa por el símbolo \mathbf{J}

Dirección

Su dirección es la misma que la del flujo de las cargas.

Magnitud

Corriente por unidad de área a través de una superficie colocada perpendicular al flujo , es decir, carga por unidad de tiempo por unidad de área.

Unidades

Por definición:

\dfrac{A}{m^2}

Formulación

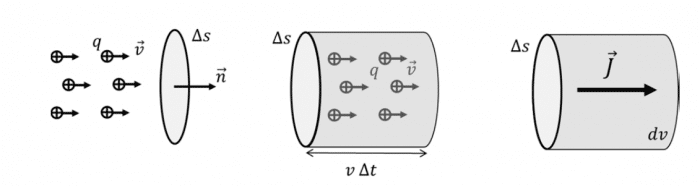
Consideramos un cilindro de seccion  \bigtriangleup s .

Por dicho cilindro circula una corriente de carga  \bigtriangleup q con velocidad \vec{v} (perpendicular a la seccion del cilindro) en un tiempo  \bigtriangleup t . Por lo tanto, teniendo en cuenta la corriente promoedio <I> y que  <J> es la corriente promedio por unidad de area:

\bigtriangleup q=<I>\bigtriangleup t=(<J>\bigtriangleup s)\bigtriangleup t

Por otro lado, teniendo en cuenta  que \rho es la denssidad de carga por unidad de volumen:

\bigtriangleup q=\rho \bigtriangleup v=\rho\bigtriangleup s<v>\bigtriangleup t .

Igualando las expresiones obtenemos la formula de la densidad de corriente volumetrica

\vec{J}=\rho \vec{v}

Podemos asi calcular la intensidad de corriente que atraviesa una superfice a traves de la densidad de corriente, por su defincion:

I=\dfrac{dq}{dt}_S=\int _S\vec{J}\cdot d\vec{s}

Densidad de corriente ELÉCTRICA SUPERFICIAL

Definición

Corriente por unidad de longitud perpendicular al flujo de carga

\vec{K}=\sigma \vec{v}

I=\int _L\left | \vec{K}\cdot\vec{t} \right |dl

SÍMBOLO

Esta densidad se representa por el símbolo \mathbf{K}

DIRECCIÓN

Su dirección es la del flujo de las cargas.

Magnitud

Corriente por unidad de longitud a través de una linea que esta sobre una superficie y colocada perpendicularmente al flujo, es decir, carga por unidad de tiempo por unidad de longitud.

Unidades

\dfrac{A}{m}

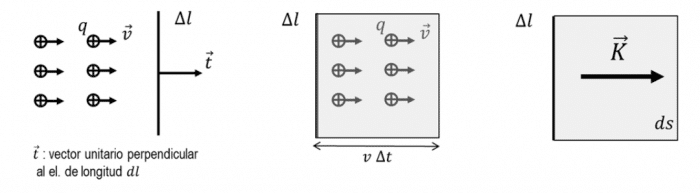
Formulación

Teniendo en cuenta una superficie

\bigtriangleup q=<I>\bigtriangleup t=(<K>\bigtriangleup s)\bigtriangleup t

Por otro lado, teniendo en cuenta  que \sigma es la densidad de carga por unidad de superficie:

\bigtriangleup q= \sigma \bigtriangleup s=\sigma \bigtriangleup lv\bigtriangleup t .

Igualando las expresiones obtenemos la formula de la densidad de corriente superficial

\vec{K}=\sigma \vec{v}

Podemos asi calcular la intensidad de corriente que atraviesa una longitud a través de la densidad de corriente, por su definición:

I=\dfrac{dq}{dt}_dl=\left | \vec{K}\cdot\vec{t} \right |dl

donde  \vec{t} es el vector unitario perpendicular al elemento de longitud. Por tanto:

I=\int _L\left | \vec{K}\cdot\vec{t} \right |dl

Ejemplos resueltos

–

Ejercicios resueltos paso a paso

Libros de Electromagnetismo
DENSIDAD DE CORRIENTE ELÉCTRICA	Potencial electrico
Energia potencial electrica	libros de electromagnetismo para estudiar
MATERIALES FERROMAGNÉTICOS