La difraccion de Fraunhofer o tambien conocida como difracción de campo lejano es un caso particular de la difracción de Fresnel, donde la pantalla esta infinitamente lejos de la fuente y del obstáculo. Es decir, la pantalla esta a una gran distancia en comparación con el tamaño del obstaculo.
Difraccion de Franhofer por una abertura rectangular con Formula
Considérese una abertura rectangular con dimensiones a\times b.
La intensidad queda como:
I(p)=I_0\left [ \dfrac{\sin(kpa/2)}{kpa/2} \right ]^2\left [ \dfrac{\sin(kpb/2)}{kpb/2} \right ]^2
Esta intensidad se anula para valores:
kpa/2=\pm u\pi
kpb/2=\pm v\pi
siendo u,v=1,2,3....
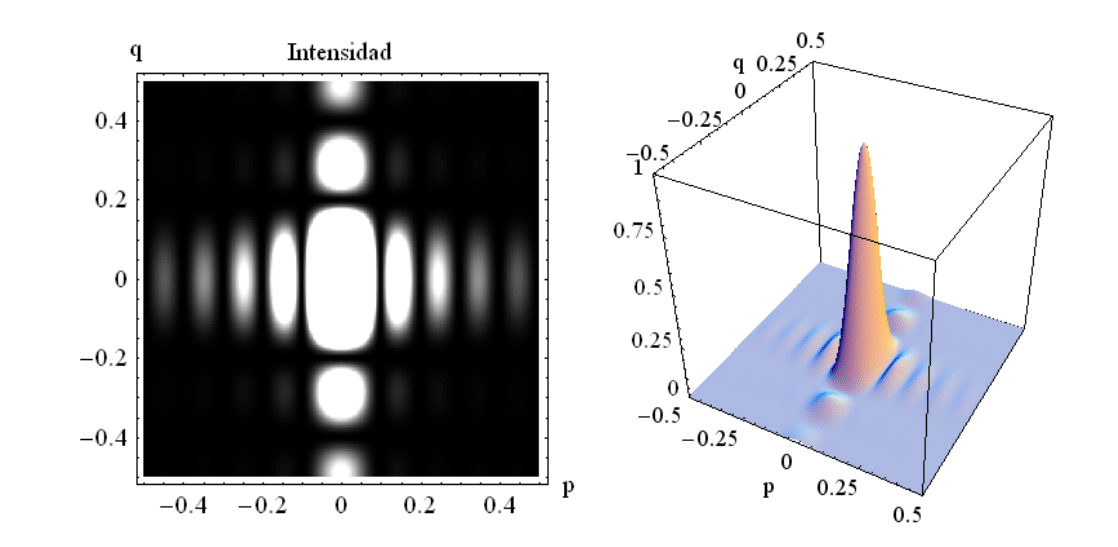
Vemos que el máximo central de intensidad es el mayor y tiene una anchura y atura dobles que el resto.
Difraccion de Franhofer por una abertura Circular con Formula
Consideremos una abertura circular cuyo radio es a.
Formula de Airy
La intensidad queda como:
I(p)=I_0\left (\dfrac{2J_1(kaw)}{kaw} \right )^2.
que es la conocida formula de Airy.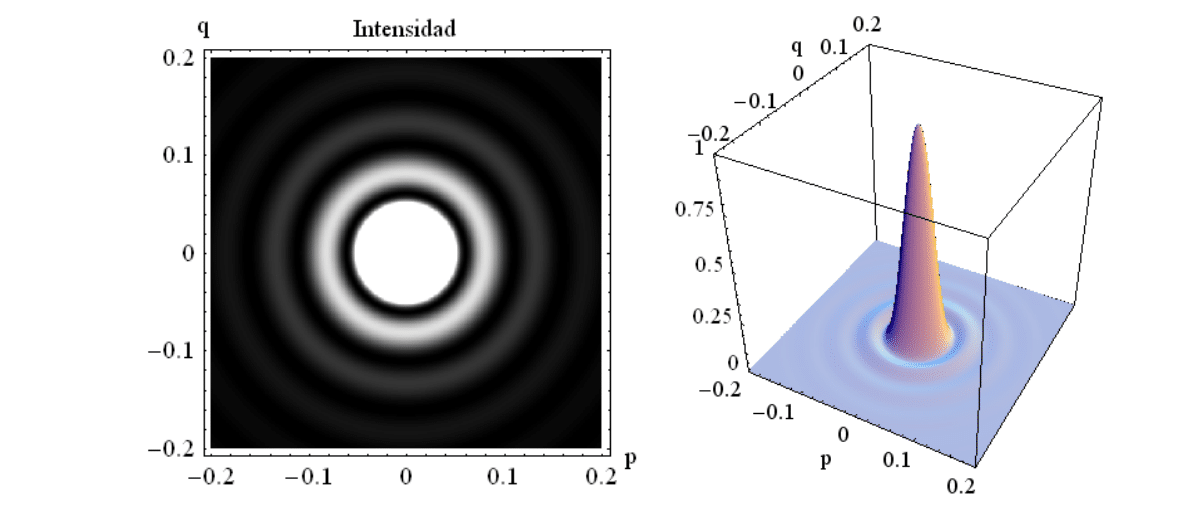
El circulo central brillante es el disco de Airy.
Difraccion de Fraunhofer por una Doble Abertura con Formula
Estudiamos el caso donde las aberturas son rectangulares. La intensidad queda como:
I(p)=4I_0\left [ \dfrac{\sin(kpa/2)}{kpa/2} \right ]^2\left [ \dfrac{\sin(kpb/2)}{kpb/2} \right ]^2\delta \cos^2(\delta /2)
Difracción de Fraunhofer por N rendijas. Red de difracción
Aquí dejamos la explicación de la red de difracción con ejercicios resueltos.
Difraccion de fraunhofer Ejercicios resueltos Optica
Ejercicio 1- Calcular los máximos y mínimos de difracción de Fraunhofer por un doble rendija iluminada por una onda plana en incidencia normal. La anchura de las rendijas es un quinto de la separación entre ellas
Como es una doble rendija la intensidad es:
I(p)=4I_0\left [ \dfrac{\sin(kpa/2)}{kpa/2} \right ]^2\left [ \dfrac{\sin(kpb/2)}{kpb/2} \right ]^2\delta \cos^2(\delta /2)
Como la anchura de las rendijas es muy pequeña con respecto a a, la intensidad queda (haciendo un limite de b\rightarrow 0)
I(p)=4I_0\left [ \dfrac{\sin(kpa/2)}{kpa/2} \right ]^2 \delta \cos^2(\delta /2)
Los máximos serán cuando:
\cos^2(\delta /2)=1
\dfrac{\delta }{2}=\dfrac{kpd}{2}=m\pi
p_M=m\dfrac{\lambda}{d}
Los minimos serán cuando:
\sin(kpa/2)=
\dfrac{kpa}{2}=m\pi
p_M=\dfrac{\lambda}{a}
