El fenómeno de la difracción se puede resumir como el efecto de una modificación del frente de ondas en su propagación. Una de las maneres mas simples de producir esta modificacion es con la ayuda de un diafragma o abertura similar. En esta ocasion vamos a estudiar en fenómeno de la difraccion de Fresnel o difracción de campo cercano.
Explicación de la difraccion de Fresnel
Consideremos una fuente emisora situada en el punto P_0=(x_0,y_0,z_0) , un punto de observacion situado en el punto P=(x,y,z) y por ultimo un objeto con una abertura A situado entre ambos puntos. (Ver figura)
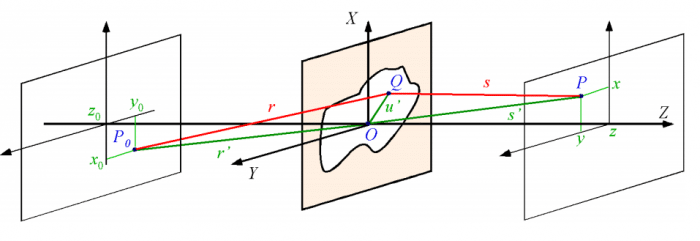
Empezemos el estudio con la integral de Fresnel-Kirchoff (no hace falta entenderla al completo, solo es nuestro punto de partida)
U(P)=-\dfrac{iU_0}{2\lambda}\int_A\dfrac{e^{ik(r+s)}}{rs}\left [ cos(\vec{n},\vec{s})-cos(\vec{n},\vec{r})\right ]d\sigma
Hacemos una serie de aproximacion (no hace falta entenderla) y llegamos a
U(P)\simeq -\dfrac{iU_0}{2\lambda}\dfrac{1}{r's'}\int_Ae^{ik(r+s)}d\sigma
Tomamos un punto en la abertura Q=(\xi,\eta ,0) (Este es un punto medido en el sistema de referencia de la abertura) y obtenemos
r^{'2}=x^{2}_0+y^{2}_0+z^{2}_0
s^{'2}=x^{2}+y^{2}+z^{2}
r^2=(x_0-\xi)^2+(y_0-\eta)^2+z^{2}_0
s^2=(x-\xi)^2+(y-\eta)^2+z^2
Por lo tanto
r=\left [ r{`2}-2(x_0\xi+y_0\eta)+\xi^2+\eta^2 \right ]^{\frac{1}{2}}
s=\left [ s{`2}-2(x\xi+y\eta)+\xi^2+\eta^2 \right ]^{\frac{1}{2}}
Aproximamos que \xi y \eta son mucho mas que pequeños ques` y r` y obtenemos la integral para la difraccion de Fresnel
Formula para la difraccion de Fresnel
U(P)\simeq -\dfrac{iU_0}{2\lambda}\dfrac{1}{r's'}\int_Ae^{ikf(\xi,\eta)}d\sigma
Esta es la integral que usaremos para resolver los problemas de difraccion de Fresnel
con
f(\xi,\eta)=(l_0-l)\xi+(m_0-m)\eta+\dfrac{1}{2}\left [ \left ( \dfrac{1}{r`}+ \dfrac{1}{s`}\right )\left ( \xi^2+\eta^2 \right ) \right ]
l_0={x_0}/{r`}
l={x}/{s`}
m_0=-{y_0}/{r`}
m={y}/{s`}
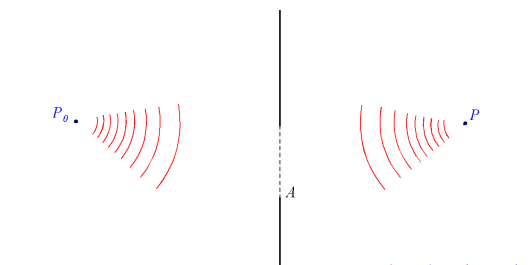
Ejemplos y ejercicios resueltos de difraccion de Fresnel con abertura circular
Sea una fuente luminosa que emite con longitud de onda \lambda . Se coloca un diafragma circular de radioa a una distancia d. Estudia los máximos y mínimos de la intensidad por la difraccion de Fresnel ocurrida en un punto situado a una distancia b del diafragma.
Adaptamos nuestra integral al ejercicio (ver imagen)
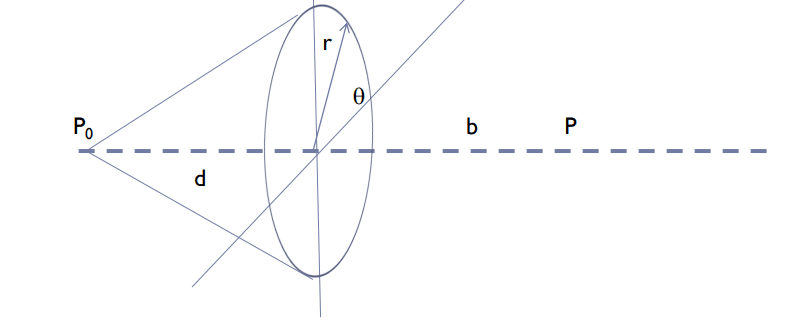
U(P)\simeq -\dfrac{iU_0}{2\lambda}\dfrac{1}{r's'}\int_Ae^{ikf(\xi,\eta)}d\sigma
Llegando a
U(z=b)\simeq U_0\dfrac{e^{eib}}{ib\lambda}\dfrac{eid}{d}\int\int_Ae^{ik^{\frac{(x^2+y^2)}{2b}}e^{ik^{\frac{(x^2+y^2)}{2d}}}}dxdy
Tenemos que calcular la integral, para ello lo transformamos a polares y la calculamos
U(z=b)\simeq U_0\dfrac{e^{eib}}{ib\lambda}\dfrac{eid}{d}\int\int_Ae^{ik^{\frac{(r^2)}{2b}}e^{ik^{\frac{(r^2)}{2d}}}}rdrd\theta
Hacemos la integral y llegamos a
U(z=b)=-U_0\dfrac{e^{ik(b+d)}}{(d+b)}\left [ e^{ik\frac{a^2}{2}\frac{d+b}{db}}-1 \right ]
La intensidad es igual
I(z=b)=UU^*
I(z=b)=\left (U_0\dfrac{1}{(d+b)} \right )^22\left [ -\cos\left ( k\dfrac{a^2}{2}\dfrac{d+b}{db}+1 \right ) \right ]
Mínimos
k\dfrac{a^2}{2}\dfrac{d+b}{db}=2\pi m
Máximos
k\dfrac{a^2}{2}\dfrac{d+b}{db}=(2m+1)\pi
Una vez visto la difraccion de campo cercano, es hora de ver la difraccion de campo lejano o difracción de Fraunhofer

