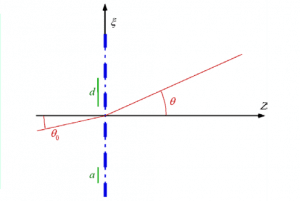
Una red de difraccion esta formada por N rendijas paralelas entre si de una anchura a y con una separación ente dos consecutivas d.
Si iluminamos la red de difracción por una onda plana formando un angulo \Theta _0 la intensidad en un punto P sera:
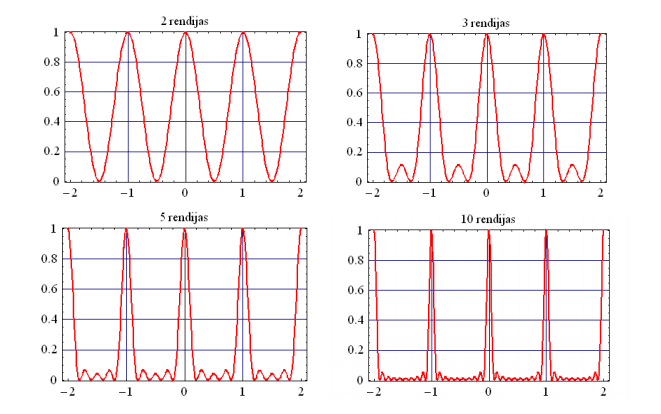
I(p)=I_0\left [ \dfrac{\sin(kpa/2)}{kpa/2} \right ]^2\left [ \dfrac{\sin(Nkpd/2)}{kpd/2} \right ]^2
El angulo con el que sale la onda despues de a travesar la red se conoce como \theta
A partir de la intensidad podemos sacar los máximos:
p=\sin\theta-\sin\theta_0=m\dfrac{\lambda }{d}
que es la conocida ecuación de una red de difracción , donde m es conocido como el orden de difraccion o orden interferencial.
También podemos obtener los mínimos:
p=\sin\theta-\sin\theta_0=j\dfrac{\lambda }{a}
En el estudio de una red de difracción también tenemos que tener el cuenta el poder de resolución:
P.R.=\dfrac{\lambda}{\Delta \lambda}=mN
La constante de la red de difracción se define como la inversa de d
cte=\dfrac{1}{d}
Red de difraccion Formula
A modo de formulario para el estudio de las redes de difracción
p=\sin\theta-\sin\theta_0=m\dfrac{\lambda }{d}
P.R.=\dfrac{\lambda}{\Delta \lambda}=mN
Red de difraccion Ejercicios resueltos Optica
Ejercicio 1. Sea una red de difracción con cte=\dfrac{1}{d}=600 \dfrac{lineas}{mm} se ilumina con luz blanca con un angulo de incidencia \Theta _0=0
a) ¿En que ángulos se difracta para los diferentes ordenes de difracción?
En este apartado no esta pidiendo los diferentes angulo de difracción \theta para los diferentes ordenes m con las longitudes de onda que comprende la luz blanca [400,700]\,nm
Para ello usamos la ecuación de la red de difracción:
p=\sin\theta-\sin\theta_0=m\dfrac{\lambda }{d}
- Para m=0
\sin\theta=\sin\theta_0=0
- Para m=1
Con una longitud de onda de \lambda=400\,nm
\sin\theta=1*\dfrac{400\,nm}{1}0,0006\,nm=0,24
\theta=\arcsin(0,24)=13,89^{\circ}
Con una longitud de onda de \lambda=700\,nm (repitiendo los calculos)
\theta=\arcsin(0,24)=24,89^{\circ}
- Para m=2
Con una longitud de onda de \lambda=400\,nm (repitiendo los calculos)
\theta=\arcsin(0,24)=28,69^{\circ}
Con una longitud de onda de \lambda=700\,nm (repitiendo los calculos)
\theta=\arcsin(0,24)=57,14^{\circ}
Una red de difracción es un caso e la difracción de Fraunhofer. Estudia los demás casos de la difracción de Fraunhofer aqui: